How-To: Decimal System

Decimal System

In the everyday life we use the Decimal System to express numbers. The Decimal System is a base ten positional system.

A base ten system means it uses 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The number 25 is made up of the digit 2 and the digit 5. This is a two digit number. The number 120 is made up of the digit 1, the digit 2 and the digit 0. This is a three digit number.
A positional (or a place value) system means each place has its own value. In the decimal system, each place value is 10 times larger than the one to its right.

Here are the place value names of the digits in a whole number. Consider the number 24 306 217 which is read “twenty four million, three hundred six thousand, two hundred seventeen”.

diagram showing the number 24,306,217 broken down into its decimal places.

Here are the place value names of the digits in the decimal number 264.39785. Recall that decimal numbers have two parts: the whole part (264) and the decimal part (39785), separated by the decimal point.

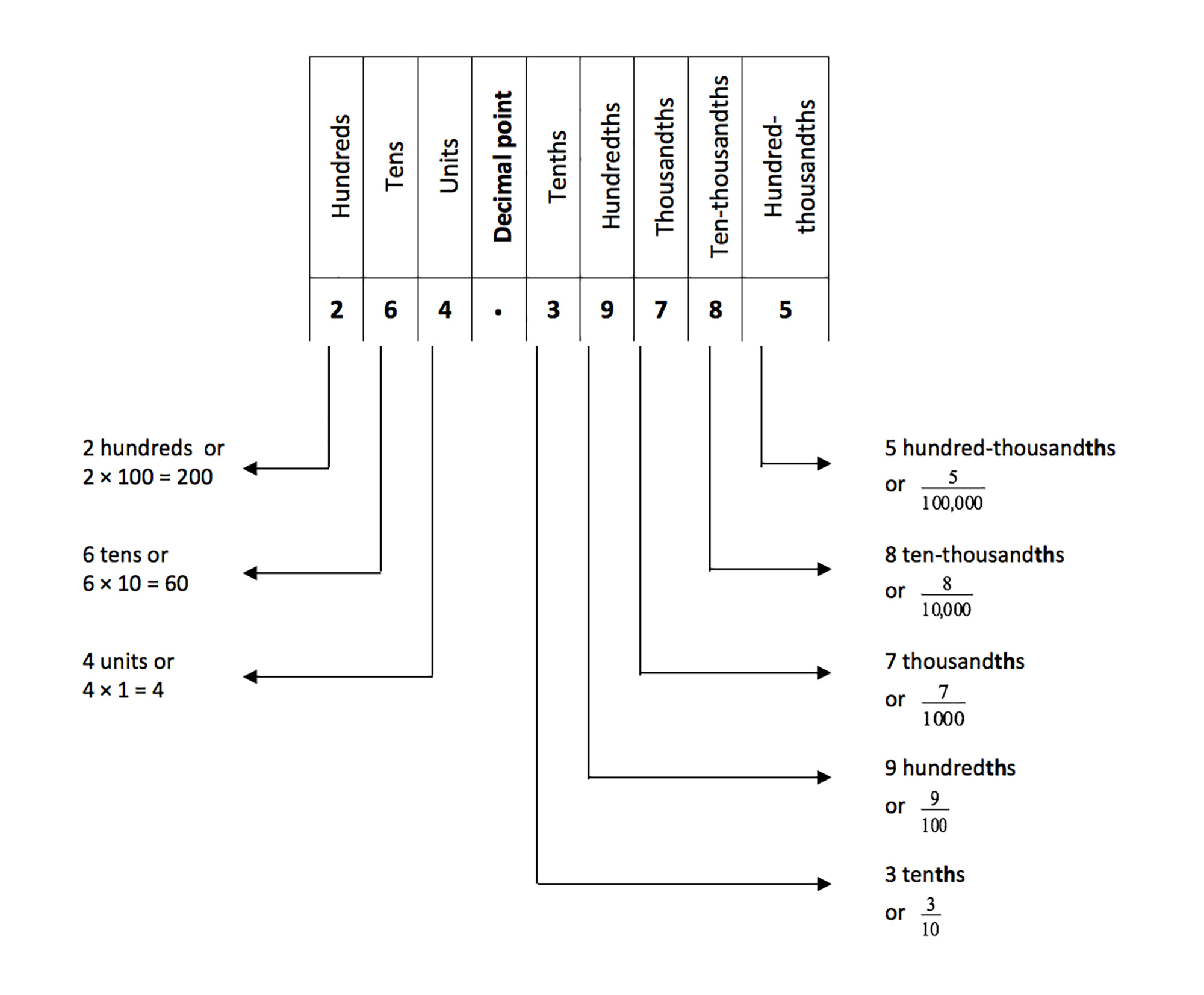
diagram showing the number 264.39785 broken down into its decimal places.

To READ a decimal number, do the following:

Read the digits to the left of the decimal place - the whole number - as normally done.
The word “and” is used in place of the decimal point.
Read the digits to the right of the decimal point as a whole number.
Read the place value name of the last digit.

Examples

Read the following decimal numbers:

$\mbox{a}) \hspace{0.5em} 15.4$

$\mbox{b}) \hspace{0.5em} 329.65$

$\mbox{c}) \hspace{0.5em} 834,207.009$

$\mbox{d}) \hspace{0.5em} 2.8340$

Solutions:

$\mbox{a}) \hspace{0.5em} 15.4$

Since $4$ is in the tenths position, $15.4$ is read ‘fifteen and four tenths'

$\mbox{b}) \hspace{0.5em} 329.65$

Since $5$, the last digit, is in the hundredths position, $329.65$ is read ‘three hundred twenty-nine and sixty-five hundredths'

$\mbox{a}) \hspace{0.5em} 834,207.009$

The decimal part is $009$ or simply $9$. But $9$ is in the thousandths position. Therefore $834,207.009$ is read ‘eight hundred thirty-four thousand two hundred seven and nine thousandths'

$\mbox{b}) \hspace{0.5em} 2.8340$

Since the last digit, $0$, is in the ten-thousandths position, $2.8340$ is read ‘two and eight thousand three hundred forty ten-thousandths’

To WRITE a decimal number, do the following:

The word ‘and’ is replaced with a decimal point. If the word ‘and’ does not appear, as in example (b) below, the whole part is understood to be zero, so, write in zero and a decimal point ($0$. ).
Write the number to the left of the word ‘and’ in its numerical form.
Determine the number of decimal places from the ending. An ending of tenths means you will have one decimal place; an ending of hundredths means two decimal places; an ending of thousandths means three decimal places, etc.
Write the number to the right of the word ‘and’ in its numerical form. You may need to include one or more zeros before the number, as shown in example (c) below, to ensure that you have the correct number of decimal places.

Examples

Write the following numbers in numerical form:

$\mbox{a}) \hspace{0.5em}$ twelve and five tenths

$\mbox{b}) \hspace{0.5em}$ seventy-three hundredths

$\mbox{c}) \hspace{0.5em}$ one hundred thirty-three and sixty-two thousandths

Solutions:

$\mbox{a}) \hspace{0.5em}$ twelve and five tenths

a) The whole part is $12$. Tenths means the decimal part has one digit. The last digit is $5$. Therefore, the number is $12.5$

$\mbox{b}) \hspace{0.5em}$ seventy-three hundredths

b) There is no “and”, so the whole part is $0$. Hundredths means the decimal part has two digits. The last digit is $3$. Therefore, the number is $0.73$

$\mbox{a}) \hspace{0.5em}$ one hundred thirty-three and sixty-two thousandths

c) The whole part is 133. Thousandths means the decimal part has three digits, and $2$ will be the last digit. Since $62$ has only two digits, we add a $0$ before $62$ to complete three digits of the decimal part. Therefore, the number is $133.062$